Astronomie

[Gilles131]

Ah, c'était le bon temps!

[Matthias]

Tontonlyco et Haflingher, un duo pétillant.
(et saoulant !)

[gma]

Tontonlyco et Haflingher, un duo pétillant.
(et saoulant !)

Heureusement qu'ils ne se faisaient pas la conversation entre eux...

[Delépine]

Si vous voulez quitter le sol en tirant vous-même vos cheveux vers le haut, ça ne marche pas.
Mais en y mêlant un peu de Relativité ce doit être différent !

David Burns de la NASA conçoit un accélérateur de particules pour les fusées spatiales | Nouvelles pour les enfants (kidsnews.com.au)

Dommage que tonton ne soit plus là ; cela aurait dû lui plaire.

[Luc Lion]

Si vous voulez quitter le sol en tirant vous-même vos cheveux vers le haut, ça ne marche pas.
Mais en y mêlant un peu de Relativité ce doit être différent !

David Burns de la NASA conçoit un accélérateur de particules pour les fusées spatiales | Nouvelles pour les enfants (kidsnews.com.au)

Dommage que tonton ne soit plus là ; cela aurait dû lui plaire.

Oui, cela aurait certainement plu à tonton, de prendre la relativité en default. Et par un ingénieur de la Nasa ; excusez du peu !

Je suis abasourdi !
Pas par la connerie puisque, après tout, elle est sensée être universelle, comme la gravité.

Je suis abasourdi que quelqu'un qui écrive de telles conneries puisse se prévaloir de la Nasa.
Ou c'est un imposteur, ou bien il vient de perdre son travail.

Le paradoxe décrit ici consiste en la non-conservation de la quantité de mouvement. Comme la plupart des paradoxes en physique, celui-ci provient d'un changement de paradigme (ici, de la physique classique vers la relativité) en appliquant de manière sélective les lois du nouveau paradigme.

Je peux démonter ce paradoxe en quelques lignes mais pas sur mon téléphone. J'ai besoin d'un ordinateur pour écrire quelques équations.

Luc

[Luc Lion]

Si vous voulez quitter le sol en tirant vous-même vos cheveux vers le haut, ça ne marche pas.

Mais en y mêlant un peu de Relativité ce doit être différent !
David Burns de la NASA conçoit un accélérateur de particules pour les fusées spatiales | Nouvelles pour les enfants (kidsnews.com.au)

Bon, je reprend le dessin présenté sur ce site, probablement par ce Monsieur Burns :




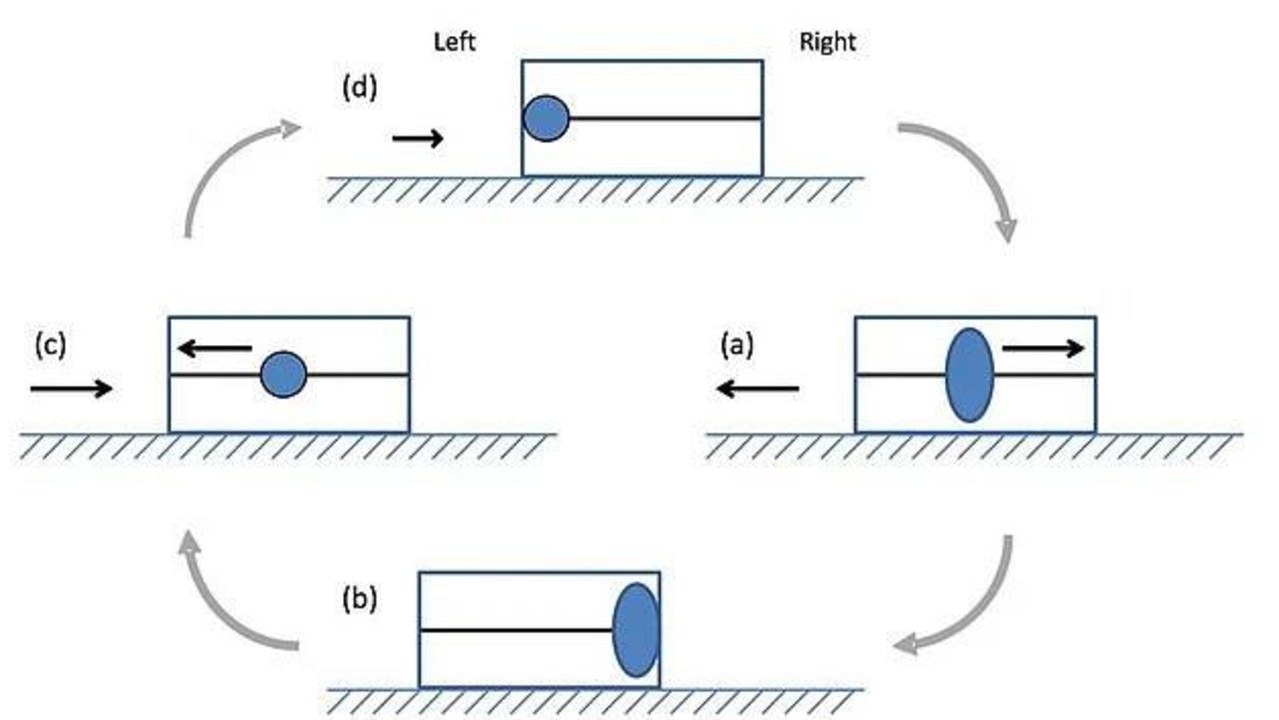
En gros, on a un système animé d'un processus cyclique, en mouvement dans le vide et n'ayant aucune interaction avec un objet externe.
Le processus cyclique est fourni par un objet interne qui vient alternativement cogner la face interne avant et la face interne arrière de l'objet composite (avant-arrière par rapport au sens de déplacement de l'ensemble).
Le postulat de l'auteur est que, si un observateur externe observe les effets de ce cycle en tenant compte des équations de la relativité restreinte, il constaterait que les chocs sur la face avant fournissent plus de quantité de mouvement que les chocs sur la face arrière à cause de l'augmentation relativiste de la masse de l'objet interne lorsque son mouvement propre se combine au mouvement de l'ensemble.
Cette différence entre les chocs avants et les chocs arrières provoqueraient une accélération de l'objet composite vers l'avant.
Cette accélération étant provoquée par un cycle répétable à l'infini, on pourrait ainsi se rapprocher indéfiniment de la vitesse de la lumière.

Ce postulat est en conflit avec le principe de la conservation de la quantité de mouvement ou seconde loi de Newton (action=réaction) car cet objet composite voit sa quantité de mouvement augmenter alors qu'il n'a d'interaction avec aucun autre objet de l'univers. Normalement, la quantité de mouvement est conservée parce que la modification de la quantité de mouvement de l'objet observé est compensée par une modification de quantité de mouvement opposée d'un autre objet avec lequel le premier interagit.
Le système du postulat n'est pas à proprement parler une "machine à mouvement perpétuel" car rien n'indique que l'augmentation de l'énergie cinétique de l'objet composite ne doit pas être compensée par une machinerie interne qui entretiendrait le mouvement de l'objet interne.

Le système décrit ici et le postulat proposé ne sont qu'un paradoxe apparent, basé sur un changement de référentiel relativiste où seule une partie des équations du changement de référentiel ont été appliquées.
En effet, je vais vous montrer que, dans tous les cas de figure, la quantité de mouvement transmise par l'objet interne à son contenant est la même sur la face arrière que sur la face avant.

Pour le montrer sur des valeurs calculées, je vais prendre l'exemple d'une objet composite avançant à 0.9 fois la vitesse de la lumière ou 0.9 c et d'un objet interne se déplaçant relativement à son conteneur à la vitesse 0.5 c. La masse au repos de l'objet interne est m0 et la masse au repos du conteneur est M0.
M0 est beaucoup plus grand que m0, ce qui nous permet de considérer que les variations de vitesse de M0 sont négligeables sur un petit nombre de cycles.
Je vais considérer que les chocs sont parfaitement élastiques, c'est à dire que les différences de vitesse entre les 2 objets avant et après le choc sont exactement opposées.
Dans les 3 cas que je vais analyser, en mécanique classique comme en mécanique relativiste, le calcul de la quantité de mouvement est le même:
   Δp = m * [(vi2 - vc2) - (vi1 - vc1)]  
où vi1 et vc1 sont les vitesses avant le chocs et vi2 et vc2 sont les vitesses après le choc, et où vi est la vitesse de l'objet interne tandis que vc est la vitesse du conteneur.
Comme le choc est élastique, on a:
   Δp = 2m * (vi - vc)

m est la masse totale, c'est à dire m0 en mécanique classique et m0 * γ en mécanique relativiste.
γ est le facteur de Lorentz γ = 1/√(1 - v²/c²)
C'est ce facteur de Lorentz qui matérialise l'augmentation de la masse relativiste avec la vitesse.
En mécanique relativiste, lorsqu'on observe un objet qui a une vitesse vi relative à un autre objet, le conteneur, et que ce conteneur a lui-même une vitesse par rapport à l'observateur, les vitesses ne s'additionnent pas simplement. Elles se composent par la formule:
   v = (vi + vc) / (1 + vi*vc / c²)
Bien sûr, si les vitesses sont faibles par rapport à la vitesse de la lumière, cette composition revient à l'addition classique.
De même, si l'une des vitesses vi ou vc est nulle, la composition dégénère aussi en une addition classique.

Premier cas: mécanique classique, observateur extérieur.
La vitesse du conteneur vaut vc = 0.9c et les vitesses de l'objet interne valent vi = 0.4c vers l'arrière et vi = 1.4c vers l'avant
Les variations de quantité de mouvement valent:
face arrière : Δp = 2m0 * (0.4c - 0.9c) = -1 m0.c
face avant : Δp = 2m0 * (1.4c - 0.9c) = +1 m0.c
Les deux variations de mouvement sont bien égales et opposées.

Deuxième cas: mécanique relativiste, observateur dans le conteneur.
La vitesse du conteneur vaut vc = 0c (l'observateur est immobile dans le conteneur).
Les vitesses relatives de l'objet interne valent vi = -0.5c vers l'arrière et vi = +0.5c vers l'avant.
Si on utilise la formule    v = (vi + vc) / (1 + vi*vc / c²) ,
on trouve aussi vi = -0.5c vers l'arrière et vi = 0.5c vers l'avant, car vc = 0
La masse m = m0 * γ = m0 / √(1 - (0.5c)²/c²) = m0 / √(3/4) = 1.1547 m0

Les variations de quantité de mouvement valent:
face arrière : Δp = 2 * 1.1547 m0 * (-0.5c) = -1.1547 m0.c
face avant : Δp = 2 * 1.1547 m0 * (+0.5c) = +1.1547 m0.c
Les deux variations de mouvement sont bien égales et opposées.
Elles sont plus élevées que dans le cas de la mécanique classique à cause de l'augmentation relativiste apparente de la masse de l'objet interne.

Troisième cas: mécanique relativiste, observateur extérieur.
La vitesse du conteneur vaut vc = 0.9c (le conteneur a une vitesse importante relative à l'observateur).
Les vitesses relatives de l'objet interne valent:
Vers l'arrière: vi = (-0.5c + 0.9c)/(1 - (0.5c*0.9c) / c²) = 0.72727c
Vers l'avant: vi = (+0.5c + 0.9c)/(1 + (0.5c*0.9c) / c²) = 0.96552c
On remarque que ces vitesses sont plus proches de la vitesse du conteneur 0.9c que dans le cas de la mécanique classique (0.4c et 1.4c).
La relativité "atténue" les variations de vitesse.
On remarque aussi que le mouvement vers l'avant se fait avec une différence de vitesse plus faible, Δv = 0.065517c, que le mouvement vers l'arrière, Δv = -0.172727c

Calculons les valeur de masse de l'objet interne lorsqu'il se déplace vers l'arrière ou vers l'avant.
Vers l'arrière: m = m0 * γ = m0 / √(1 - (0.72727c)²/c²) = m0 / √(0.47108) = 1.45699 m0
Vers l'avant: m = m0 * γ = m0 / √(1 - (0.96552c)²/c²) = m0 / √(0.06777) = 3.84114 m0
Ces valeurs semblent donner raison à Monsieur Burns ; la valeur de la masse de l'objet interne est beaucoup plus grande, 3.8411 m0, lorsqu'il se déplace vers l'avant que celle, 1.4570 m0, lorsqu'il se déplace vers l'arrière.

Calculons maintenant les variations de quantité de mouvement. Elle valent:
face arrière : Δp = 2 * 1.45699 m0 * (-0.172727c) = -0.5033 m0.c
face avant : Δp = 2 * 3.84114 m0 * (+0.065517c) = +0.5033 m0.c
Les deux variations de mouvement sont bien égales et opposées.
On voit les différences de vitesse entre les deux objet, plus faible vers l'avant que vers l'arrière, compensent exactement les différence de masse.
Les variations de mouvement sont plus faibles que dans le cas de la mécanique classique à cause de cette diminution relativiste apparente de la différence de vitesse entre les deux objets.

On trouve un résultat que l'on pouvait deviner intuitivement : changer de référentiel ne change pas la physique ; cela change uniquement les valeurs apparentes.

Luc

[Delépine]

.
A mon avis :

Si le principe fonctionne :
Un astronef muni de ce moteur (arrêté) passe à une certaine vitesse relative devant un observateur. Il démarre alors son moteur : l'observateur voit l'astronef accélérer.
Avant mise en marche du moteur, un second astronef semblable accompagne le premier avec une vitesse relative nulle. Le premier démarre son moteur. Or à vitesse nulle v/c = 0, le moteur ne pousse pas. Du second astronef, qui n'a pas démarré son moteur, on ne voit donc pas accélérer et s'éloigner le premier.
Ennuyeux !

Si le principe fonctionnait, on aurait un moyen de caractériser le repos et de le distinguer du mouvement, selon que le moteur fait ou non accélérer le vaisseau, et voilà la Relativité par terre (ce dont précisément se défend l'auteur !)

[Luc Lion]

Delépine,
est-ce que tu utilises un moteur de recherche particulier pour parvenir à trouver des âneries comme celle-ci ?

Luc

[Delépine]

Ne te prive pas de commenter.

[Luc Lion]

J'ai essayé.
Mais les commentaires doivent passer par l'approbation d'un modérateur dont la dernière visite remonte à deux ans plus tôt.

Luc

[Delépine]

Quelle cordialité !

[Yankeeromeo]

(...) Je suis abasourdi !
Pas par la connerie puisque, après tout, elle est sensée être universelle, comme la gravité.
Je suis abasourdi que quelqu'un qui écrive de telles conneries puisse se prévaloir de la Nasa. Ou c'est un imposteur, ou bien il vient de perdre son travail.
Le paradoxe décrit ici consiste en la non-conservation de la quantité de mouvement. Comme la plupart des paradoxes en physique, celui-ci provient d'un changement de paradigme (ici, de la physique classique vers la relativité) en appliquant de manière sélective les lois du nouveau paradigme.
(...)
Luc

Que voulez-vous ? Nous vivons une époque moderne...
Où la différence entre micromètre et nanomètre échappe au commun de mortels, et même à des prétendus scientifiques...
Où les ministres utilisent des brochures commerciales de certains fabricants, pour en extraire des arguments soi-disant "scientifiques", et où ils se contredisent toutes les deux semaines sans que cela gêne personne...

La seule explication de cet état de fait qui me semble convaincante est justement la-vôtre : "la connerie est censée être universelle, comme la gravité."...
Pourtant "Nous avons le droit d'être intelligents !" comme dirait l'autre.

[Delépine]

Delépine,
est-ce que tu utilises un moteur de recherche particulier pour parvenir à trouver des âneries comme celle-ci ?

Luc

Cette réponse paraissant insuffisamment argumentée, faute d'y avoir lu de quoi changer d'avis je maintiens mon commentaire.
Mais la différence avec tonton est que je ne demande qu'à changer d'avis.
Assure-toi qu'il n'y ait pas d'ambiguïté.